Bramki logiczne - symbole i zastosowanie

Bramki logiczne to podzespoły należące do grona układów cyfrowych. Bez nich, jakikolwiek współczesny układ elektroniczny w ogóle nie mógłby powstać. Jak działają i gdzie się je stosuje?

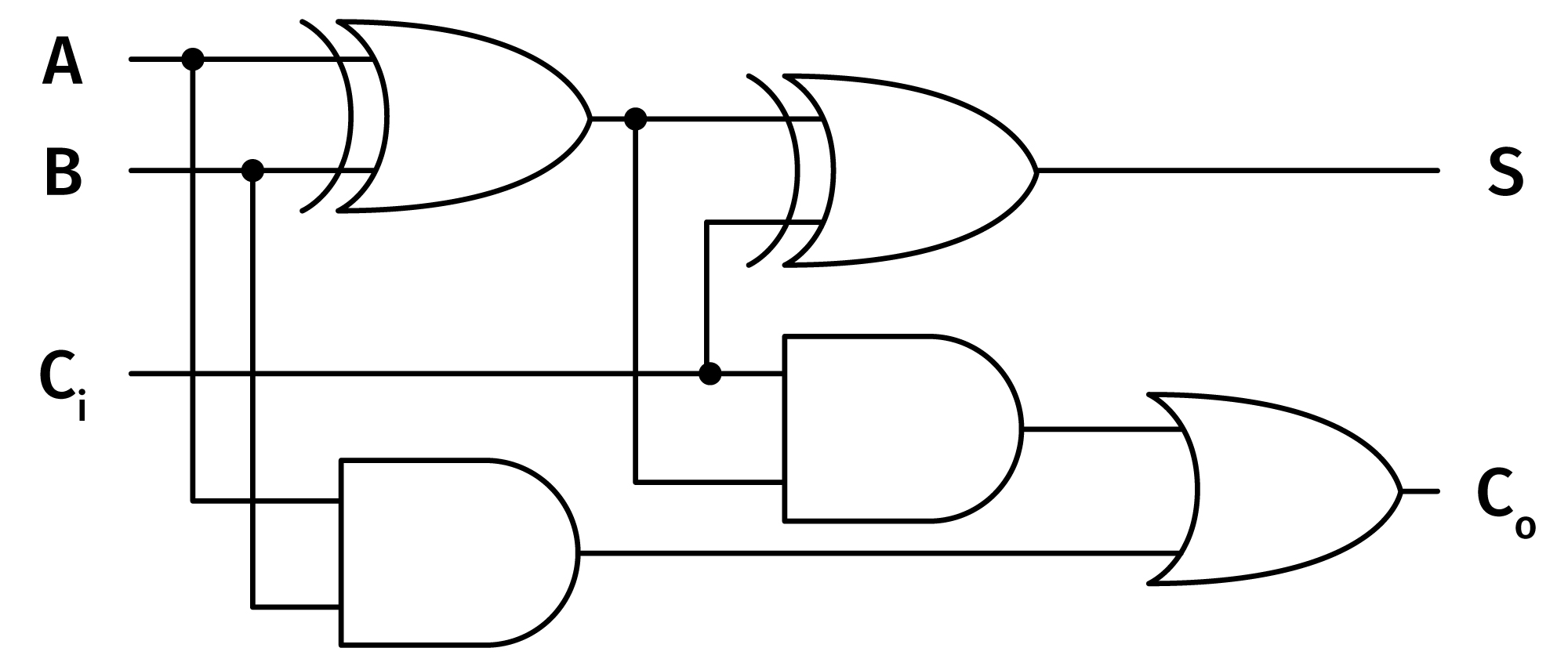
Skąd takie zapotrzebowanie?

Elektronika cyfrowa, którą otaczamy się na co dzień, przetwarza sygnały w postaci binarnej, czyli przyjmującej jedną z dwóch wartości. Robi to na wiele różnych sposobów oraz bardzo szybko. Komputer, smartfon, zegarek, a nawet sterownik piekarnika czy pralki automatycznej - to wszystko są urządzenia cyfrowe.

Aby zrozumieć podstawy ich działania, sięgnijmy do XIX wieku. To tam ma podwaliny cały świat współczesnej elektroniki.

Geneza

George Boole, angielski filozof i matematyk, stworzył zupełnie nowy obszar matematyki, zwany algebrą Boole’a - od jego nazwiska. Ciekawe w nim jest to, że każdy element może przyjmować tylko jedeną z dwóch dopuszczalnych wartości:

• 1 - rozumiany też jako “prawda”
• 0 - czasem nazywany “fałszem”

Wraz z nimi Boole podał zbiór możliwych operacji, jakie można na nich wykonywać. Tworzą kompletny, zwarty zbiór działań. Jednak nie przypuszczał, że teoria przez niego opracowana będzie w przyszłości tak szeroko wykorzystywana.

Czy to ma jakieś zastosowanie?

Ktoś mógłby zapytać: po co to komu? Przecież ta teoria powstała prawie 200 lat temu, dzisiaj wszystko jest nowocześniejsze! Problem w tym, że nie wszystko. Niektóre rzeczy, jak wspomniana już algebra Boole’a, pozostały niezmienione. I są intensywnie wykorzystywane do dzisiaj.

Boole rozpisywał działania na tablicy lub kartce papieru. Odpowiednie uporządkowanie działań pozwalało na uzyskanie prawidłowego wyniku. A gdyby tak te działania mogły wykonywać się… same? I w dodatku bardzo szybko, miliony razy na sekundę? Do tego służą nam bramki logiczne.

Elektronika cyfrowa - podstawy

Aby zrozumieć, jak działają i do czego służą bramki cyfrowe, najpierw trzeba poznać podstawowe prawa rządzące elektroniką cyfrową. To taka gałąź tej dziedziny nauki, która zajmuje się sygnałami przyjmującymi jedynie dwie możliwe wartości - wspomniane już 1 oraz 0.

1 możemy traktować jako np. zamknięcie drzwi, zaś 0 jako ich otwarcie. Albo 1 to wychwycenie jakiejś transmisji, a 0 oznacza jej brak. Jednak jak to wyjaśnić układowi elektronicznemu, składającemu się z diod i tranzystorów?

Reprezentacja

W zdecydowanej większości przypadków wartości logiczne - bo tak nazywamy zero i jedynkę - są reprezentowane przez odpowiednie wartości napięć. W niektórych standardach (bo jest ich dzisiaj naprawdę wiele) zostały podane wprost przedziały wartości, a niekiedy są to ułamki odniesione do wartości napięcia zasilającego. Tak na przykład ma bardzo popularna rodzina układów CMOS.

Jeżeli napięcie w danej linii mieści się w przedziale od 0 do 30% napięcia zasilającego, interpretujemy je jako 0. Górny zakres, od 70% do 100% napięcia zasilania, oznacza 1. Przedział od 30% do 70% uznajemy za stan zabroniony - nie wiadomo, jak układ zinterpretuje takie napięcie wejściowe, a nawet może ulec uszkodzeniu.

Rola bramek

Same napięcia, występujące na odpowiednich przewodach, nie nadają się do niczego. Bramki służą do przetwarzania tych napięć zgodnie z działaniami określonymi we wspomnianej już algebrze Boole’a. Wszystkie układy cyfrowe posługują się nią.

Bramki to niewielkie układy elektroniczne, złożone najczęściej z tranzystorów, które realizują funkcje logiczne na podanych wartościach wejściowych. Każda bramka podaje wynik operacji na swoim wyjściu w tym samym standardzie, w którym dostała wartości wyjściowe. Bramki można zestawiać kaskadowo, czyli wyjścia jednych łączyć z wejściami innych. Ale o tym dalej.

Rodzaje bramek

Elektroniczne funktory logiczne, czyli bramki cyfrowe, realizują określone operacje, zgodnie z prawami opisanymi przez Boole’a. Trzy z nich są podstawowe i umożliwiają stworzenie dowolnego układu logicznego:

• NOT
• AND
• OR

Pozostałe wynikają z ich złożenia, ale również są bardzo często stosowane. Niekiedy nawet częściej od swoich pierwowzorów:

• NAND
• NOR
• XOR (EXOR)
• XNOR (EXNOR lub NXOR)

Każda z nich zostanie oddzielnie omówiona. Dla porządku proponuję przyjąć, że A i B oznaczają zmienne wejściowe, a Q, X, Y lub Z - zmienną wyjściową. Bramka przetwarza (w charakterystyczny dla siebie sposób) zmienne wejściowe na wyjściową. Każda bramka zawsze posiada tylko jedno wyjście, choć istnieją pewne wyjątki.

NOT

To najprostsza z bramek logicznych, zwana negatorem. Posiada jedno wejście i jedno wyjście. Jej zadaniem jest zmiana wartości logicznej na przeciwny: kiedy na wejściu dostaje 1, na swoim wyjściu wystawia 0. Analogicznie, po otrzymaniu sygnału reprezentującego 0, wyjście przyjmuje wartość 1.

Działanie negacji jest jednoargumentowe, co oznacza, że tylko jedna zmienna jest argumentem tej funkcji. Funkcję tę oznacza się zwrotem NOT lub znakiem tyldy (~). W zapisach matematycznych jest również stosowane nadkreślenie, czyli pozioma linia nad nazwami argumentów.

~1 = 0

~0 = 1

Symbol tej bramki to trójkąt z niewielkim kółeczkiem na wierzchołku. Właśnie to kółeczko oznacza negację. Dociekliwi mogą zauważyć, że znajdujący się w symbolu bramki trójkąt oznacza również wzmacniacz - i będą mieli rację!

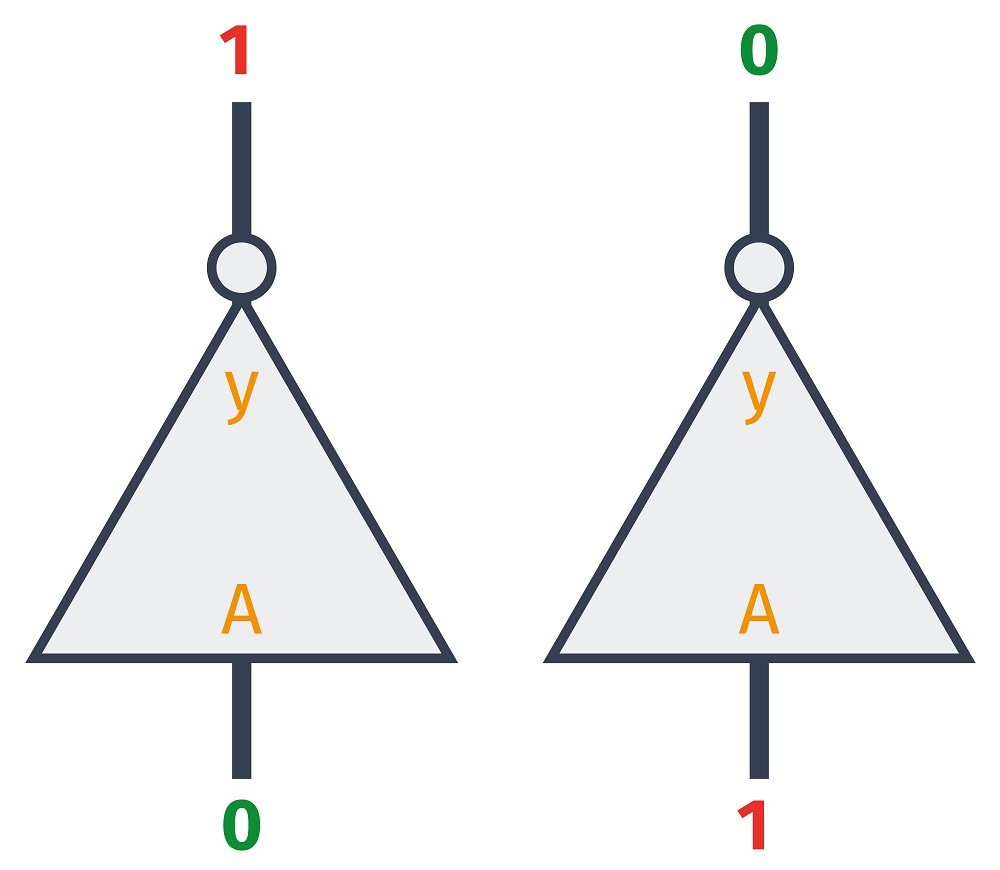
Każda bramka ma właściwość wzmacniania podanego na nią sygnału, a bramka NOT jest w tym charakterystyczna o tyle, że posiada wyłącznie jedno wejście.

AND

Rolą tej bramki jest tworzenie iloczynu logicznego. Jej wyjście ustawi się w stanie 1 tylko wtedy, kiedy wszystkie jej wejścia znajdą się w stanie 1. Podanie wśród tych jedynek jakiegokolwiek zera spowoduje wyzerowanie wyniku. Symbolem funkcji AND może być również krzyżyk (×) lub kropka (⋅) które pochodzą od matematycznego zapisu operatora mnożenia. W programowaniu często używa się znaku &.

0 ⋅ 0 = 0

1 ⋅ 0 = 0

0 ⋅ 1 = 0

1 ⋅ 1 = 1

083_06

Ta bramka ma dwa wejścia lub więcej - istnieją w sprzedaży układy zawierające bramki o 3, 4 lub nawet 8 wejściach. Jednak zasada działania jest za każdym razem taka sama, bowiem chodzi o ustawienie wszystkich wejść w stanie wysokim (czyli 1).

Jej symbol ma półokrągłe zakończenie. Wejścia są z jednej strony, wszystkie równoległe do siebie, a wyjście z drugiej.

Iloczyn logiczny jest niezbędny do stwierdzenia, czy wszystkie zmienne wejściowe znajdują się w stanie wysokim. Jeżeli to prawda - bramka potwierdza to jedynką na wyjściu. Jeżeli którykolwiek z nich nie jest - wystawia zero.

OR

OR to logiczna suma. Wystawia na wyjściu 1 wtedy, kiedy którakolwiek ze zmiennych wejściowych przyjmuje stan 1. Jeżeli wszystkie przyjmą stan wysoki, wyjście nadal jest równe 1. Dopiero wtedy, kiedy wszystkie wejścia zostaną wyzerowane, również stan wyjścia spada do zera. Symbolem funkcji OR może być również znak dodawania (+) który pochodzi z matematyki. W programowaniu często używa się znaku I (pionowa kreska, nie wielkie “i”, ani też nie mała litera “L).

0 + 0 = 0

1 + 0 = 1

0 + 1 = 1

1 + 1 = 1

Ta bramka również może mieć dowolną liczbę wejść - 2, 3, 4 i więcej. Jej symbol wygląda nieco inaczej niż bramki AND, ponieważ ma szpiczaste zakończenie i jest wklęsła od strony wejść.

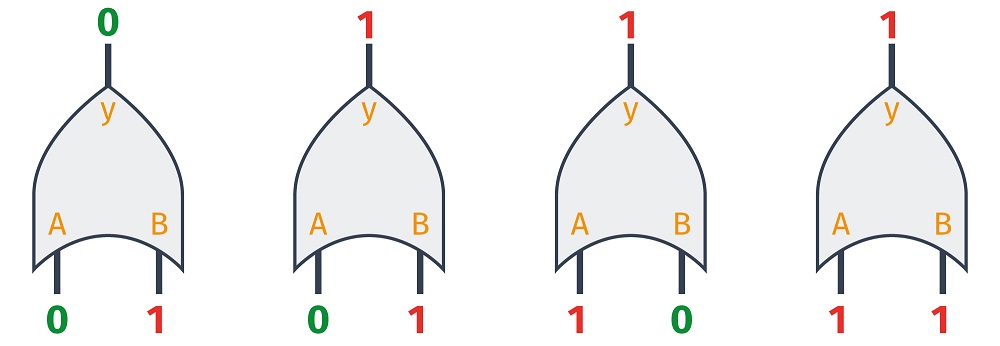
Suma logiczna pozwala określić, czy jakakolwiek zmienna wejściowa jest w stanie wysokim. Warto przy tym zauważyć, że funkcja OR nie jest jedynie zanegowaną wersją funkcji AND. Tak mogłoby się wydawać na pierwszy rzut oka, lecz proste porównanie pozwala zauważyć różnicę w działaniu:

Dla bramki AND

1 ⋅ 0 = 0

1 ⋅ 1 = 1

083_10

Dla bramki OR

1 + 0 = 1

1 + 1 = 1

Nie da się zbudować bramki OR wyłącznie z bramek AND i odwrotnie. Dopiero mając negator (NOT) jest to możliwe, czyli z bramek AND i NOT zrobić OR oraz z OR i NOT zrobić AND.

NAND

Ta bramka jest pochodną AND i ma zanegowane wyjście. Jej nazwa pochodzi od skrótu Not AND. Symbol tej bramki różni się dodatkowym kółeczkiem przy wyjściu - jak u bramki NOT.

~(0 ⋅ 0) = 1

~(1 ⋅ 0) = 1

~(0 ⋅ 1) = 1

~(1 ⋅ 1) = 0

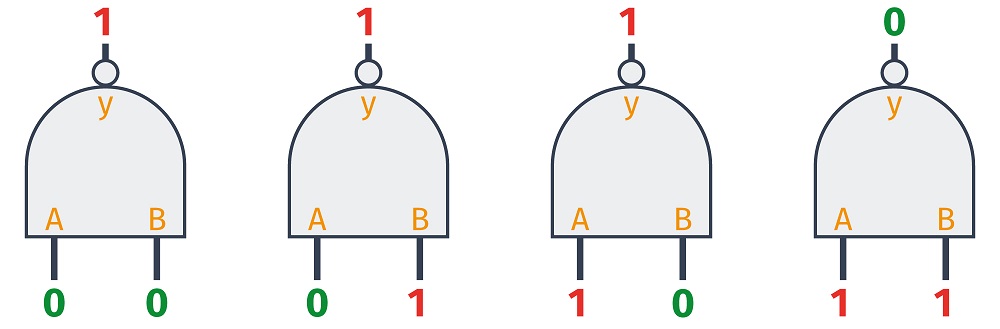
Negacja wyjścia oznacza, że tylko w jednej sytuacji da nam swoim wyjściu zero - kiedy wszystkie wejścia mają wysoki stan logiczny. W jakiejkolwiek innej sytuacji, stan wyjścia wynosi 1.

Co ciekawe, z bramek NAND można zbudować każdy inny funktor logiczny: NOT, OR, AND oraz bardziej złożone układy.

NOR

Ta bramka wywodzi się z funktora OR i, podobnie jak NAND, różni się od pierwowzoru zanegowanym wyjściem. Symbol bramki NOR różni się od OR kółkiem przy wyjściu.

~(0 + 0) = 1

~(1 + 0) = 0

~(0 + 1) = 0

~(1 + 1) = 0

Zanegowanie jej wyjścia powoduje, że przyjmuje ono stan niski zawsze wtedy, kiedy na jakimkolwiek wejściu pojawi się jedynka. Wysoki stan logiczny wyjścia jest możliwy wyłącznie po wyzerowaniu wszystkich wejść.

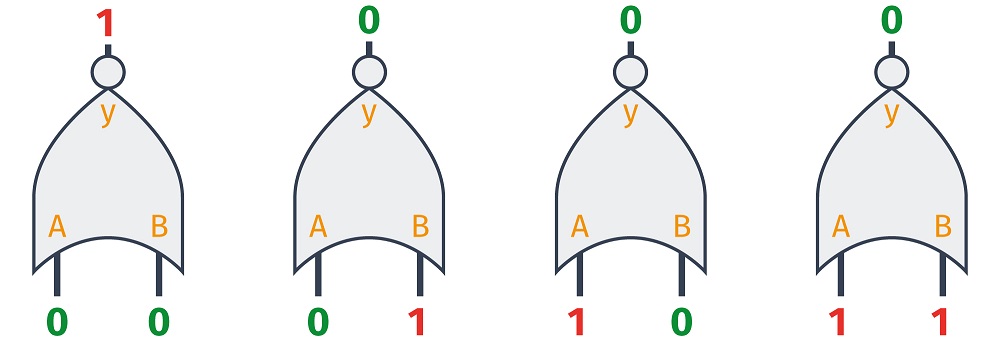
Bramki NOR, podobnie jak NAND, również są uniwersalne. Można z nich stworzyć każdy inny funktor logiczny.

XOR (EXOR)

Ta bramka działa zupełnie inaczej niż poprzednie. Exclusive-OR, czyli alternatywa wyłączająca, jest działaniem dwuargumentowym. Jej działanie najprościej można opisać stwierdzeniem “suma modulo 2” - czyli wystawia na wyjściu resztę z dzielenia sumy przez 2.

Jej symbol jest podobny do bramki OR, z jedną różnicą - ma podwójną linię od strony wejść. Symbolem tego działania logicznego jest znaczek + umieszczony w okręgu, czyli ⊕.

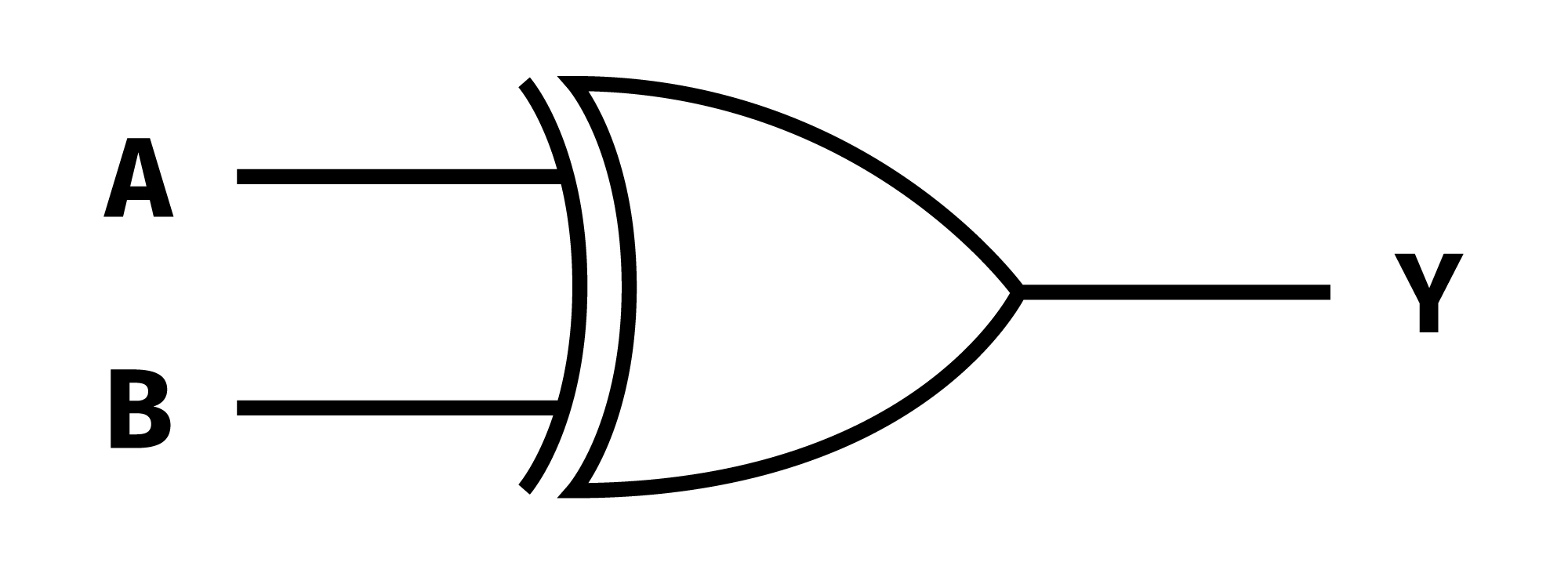
Najprościej wyjaśnić jej działanie na przykładzie.

0 ⊕ 0 = 0

1 ⊕ 0 = 1

0 ⊕ 1 = 1

1 ⊕ 1 = 0

083_17

Trzy pierwsze wiersze pokazują działanie tej bramki jak zwykłego funktora OR. Jednak w momencie, kiedy oba wejścia przyjmą ten sam stan wysoki (ostatnia sytuacja), wyjście ulega wyzerowaniu. Można to również zrozumieć jak resztę z dzielenia sumy liczb wejściowych (1 + 1) przez 2. 1+1 = 2, więc dzieli się przez 2 bez reszty, stąd zero.

Te bramki są bardzo często stosowane w różnego rodzaju układach kryptograficznych oraz generujących sumy kontrolne na podstawie ciągu bitów. Można powiedzieć, że pełnią szalenie ważną funkcję w dzisiejszym świecie, mimo, iż nie należą do “kanonu” bramek.

XNOR (EXNOR lub NXOR)

Ta bramka to po prostu XOR z zanegowanym wyjściem. Ustawia je w stan wysoki tylko wtedy, kiedy oba argumenty wejściowe mają taką samą wartość logiczną.

~(0 ⊕ 0) = 1

~(1 ⊕ 0) = 0

~(0 ⊕ 1) = 0

~(1 ⊕ 1) = 1

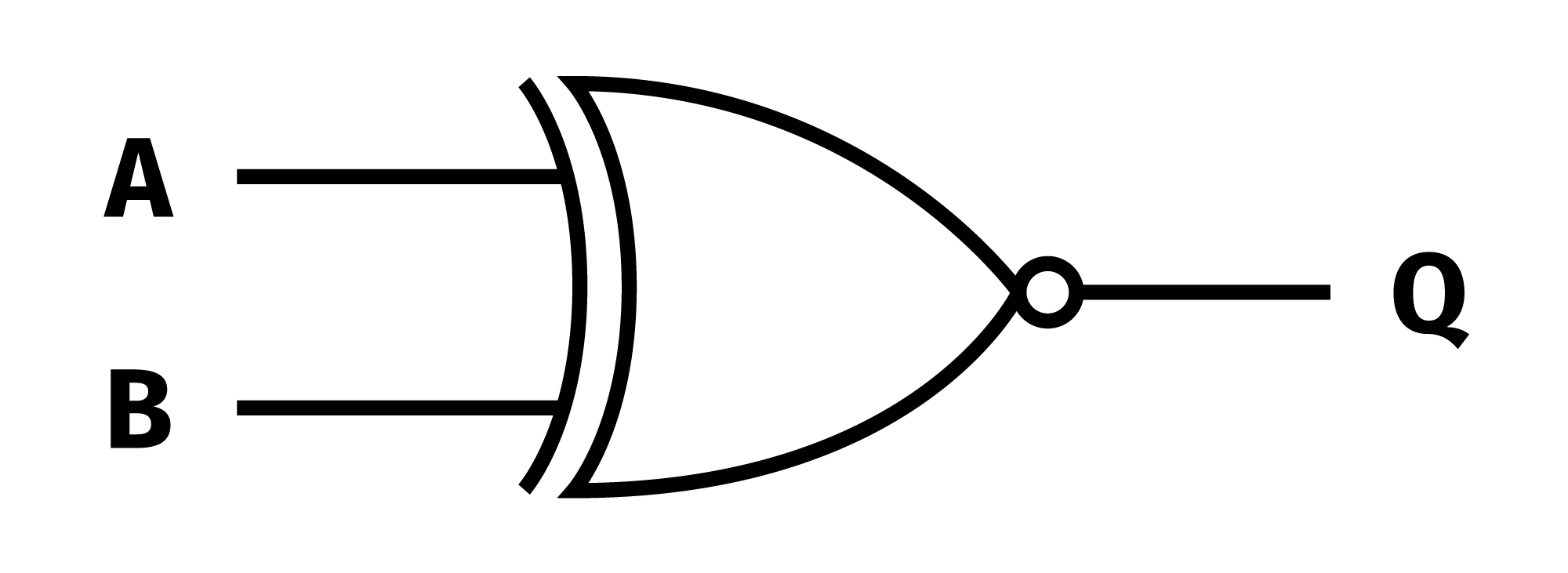
Zarówno z bramek XOR, jak i XNOR, można złożyć wszystkie inne funktory logiczne.

Zestawienie

Poniższa tabela zawiera wszystkie wymienione wyżej informacje “w pigułce”, czyli:

• nazwę każdej bramki,
• matematyczny zapis realizowanej operacji,
• symbol schematowy,
• tabelę prawdy.

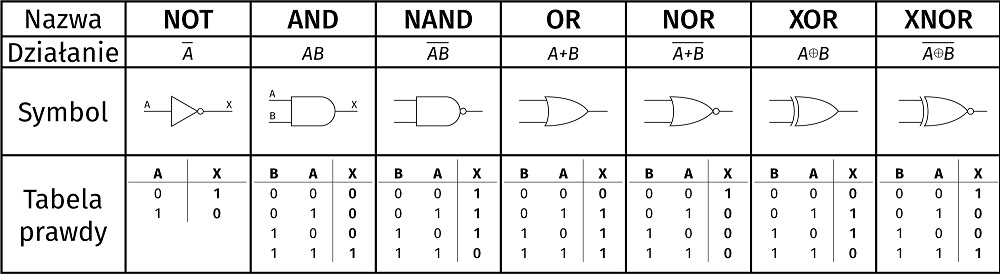
Modyfikacje

Bramki logiczne (zwane również cyfrowymi) występują w różnych odmianach. Oto kilka z nich.

Wejścia Schmitta

W sprzedaży są dostępne układy posiadające wejścia opatrzone przerzutnikami Schmitta. Skrótowo nazywa się je bramkami z wejściami Schmitta. Realizowane przez nie funkcje są identyczne jak w pierwowzorach, zasadnicza różnica odnosi się do obsługiwanych poziomów napięć wejściowych.

Pokazany wcześniej standard CMOS, który reprezentuje stany logiczne napięciami mieszczącymi się w odpowiednich przedziałach, ma przedział zabroniony. Podanie na wejście bramki napięcia mieszczącego się w przedziale zabronionym może wywołać jej chaotyczne zachowanie lub nawet ją zniszczyć. W rzeczywistości taka sytuacja może wystąpić dosyć często, na przykład kiedy przesyłamy informację przez długie przewody. Indukujące się w nich zakłócenia mogą mieć amplitudę mieszczącą się w przedziale zabronionym.

Rozwiązaniem jest wprowadzenie pewnej strefy nieczułości każdego z wejść, czyli histerezy. Zmiana stanu na 1 wymaga podania napięcia wyższego niż próg górny, zaś na 0 - niższego niż próg dolny. Wartości tych progów są różne. Jeżeli napięcie wejściowe jest pomiędzy tymi przedziałami, nie dzieje się nic - bramka nie reaguje. Obrazowo przedstawia to taki wykres, zawierający pętlę. Ten jest dla bramki NOT.

//przerysować https://images.app.goo.gl/KZVfK9JxZRAeXgabA z polskimi opisami: Vin = Uwe, Vout = Uwy, Low = 0, High = 1, Switching Point Input Falling = próg dolny, Switching Point Input Rising = próg górny, Hysteresis = histereza

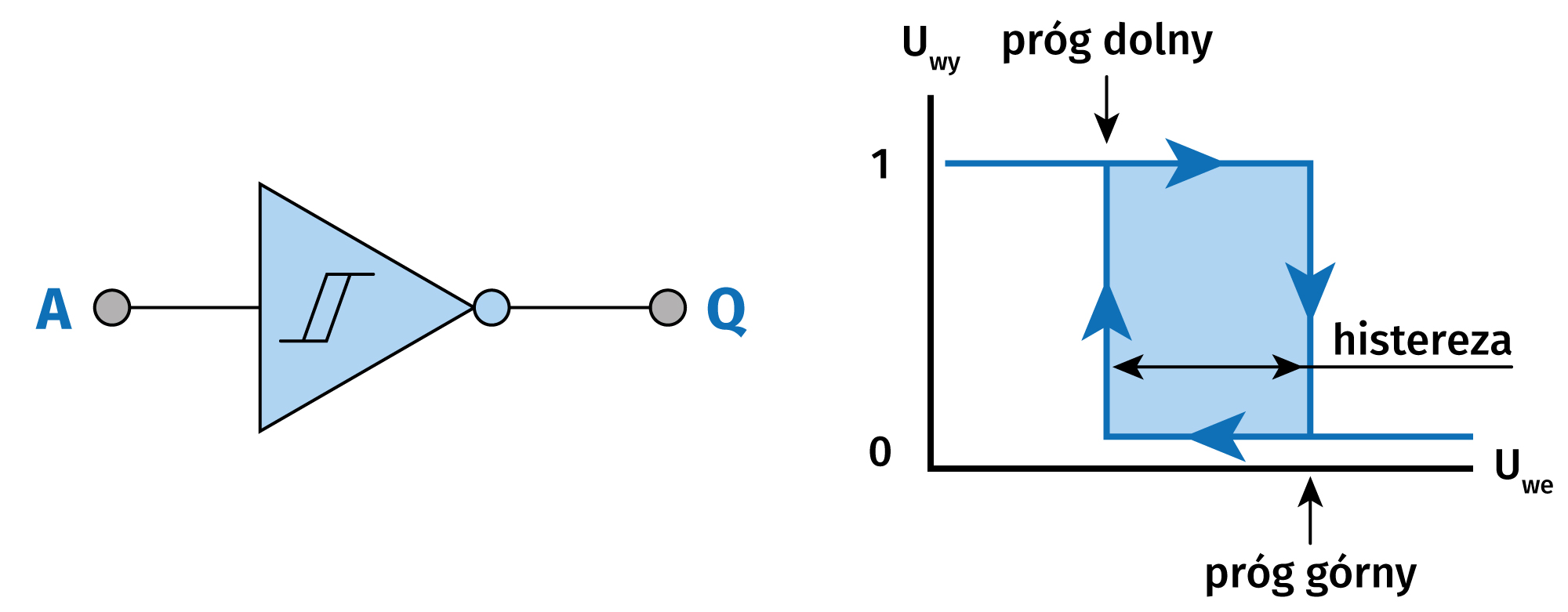
Dla niskiego napięcia wejściowego mamy stan wysoki na wyjściu. Przesuwając się w prawo, kiedy napięcie wejściowe rośnie, dochodzimy do górnego progu przerzutu (zgodnie ze strzałkami), kiedy napięcie wyjściowe gwałtownie spada. Dalszy wzrost napięcia na wejściu nic już nie zmieni, bramka zmieniła stan wyjścia na 0.

Idąc w drugą stronę, kiedy napięcie wejściowe spada, bramka utrzymuje stan niski tak długo, jak długo napięcie wejściowe znajduje się powyżej dolnego progu przerzutu. Po jego przekroczeniu, napięcie wyjściowe wzrasta, przyjmując logiczny stan 1. Pomiędzy progami przerzutu znajduje się obszar histerezy, czyli nieczułości,, kiedy to bramka nie wykonuje zmian stanu napięcia wyjściowego.

Wejście Schmitta oznacza się schematycznym rysunkiem tzw. pętli histerezy wewnątrz symbolu bramki. Każda z wyżej opisanych bramek może występować w wersji zarówno z wejściami zwykłymi, jak i Schmitta.

Inne technologie

Dotychczas została omówiona jedynie technologia CMOS, która jest dzisiaj najczęściej stosowana, lecz nie jest jedyna. Zawiera tranzystory unipolarne, zatem nie pobiera prądu w stanie spoczynku. To najważniejsza cecha, dzięki którym jest dzisiaj szeroko stosowana w wielu odmianach. Ale istnieją też inne.

TTL - Transistor-Transistor Logic - to historycznie pierwsza rodzina układów cyfrowych. Była wykonana w oparciu o tranzystory bipolarne. Przystosowana do zasilania napięciem 5V lub zbliżonym. Pobierała stosunkowo dużo prądu i była dosyć wolna. Powstała w latach 60’ XX wieku, więc jest już leciwa. Coraz rzadziej spotyka się układy wykonane w ten sposób, producenci półprzewodników częściej wypuszczają na rynek zamienniki tych układów wykonane na tranzystorach unipolarnych.

Schemat bramki NAND w standardzie TTL przedstawia poniższy schemat. Jedna bramka potrafiła pobierać prąd o natężeniu nawet kilkunastu miliamperów.

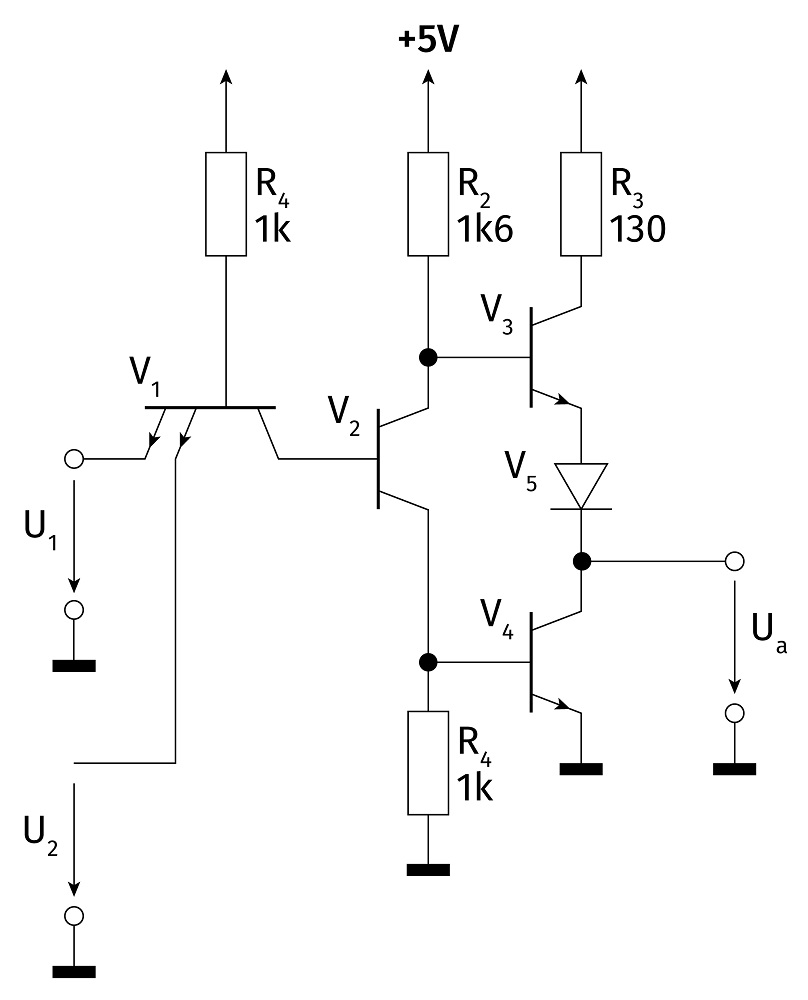
Seria TTL doczekała się wielu modyfikacji, jak F czy LS - wszystko to miało na celu zwiększenie szybkości działania tych układów. Dzisiaj określeniem TTL określa się standard napięć, w którym logiczne 0 odpowiada napięciu bliskiemu 0V, a logiczny poziom 1 - bliski napięciu zasilania.

ECL - Emitter Coupled Logic - całkowicie zmieniono podejście do bramek cyfrowych. Zawierają w swojej strukturze wyłącznie wzmacniacze różnicowe, w których tranzystory bipolarne pracują w obszarze liniowym (aktywnym) bądź zatkania. To było piętą achillesową serii TTL, w której tranzystory wchodziły w stan nasycenia - wychodzenie z tego stanu jest relatywnie wolnym procesem. Nazwa wzięła się od podstawowego schematu układu różnicowego, w którym emitery tranzystorów są połączone ze sobą.

Układy serii ECL były zdecydowanie szybsze, jednak wiązało się to z wysokim poborem prądu. W odróżnieniu od układów TTL, te są produkowane do dzisiaj, ponieważ umożliwiają prowadzenie transmisji sygnałów logicznych w liniach różnicowych. To z kolei bardzo skraca czas propagacji takiej informacji oraz zwiększa odporność na zakłócenia. Dzisiejsze odmiany układów ECL to PECL lub LVPECL, które nie wymagają do działania ujemnego napięcia zasilania.

Do czego używamy bramek?

Z bramek cyfrowych są budowane wszystkie układy kombinacyjne. To układy cyfrowe, które dają odpowiedź w czasie rzeczywistym, jedynie z niewielkim opóźnieniem wynikającym z czasu przełączania się tranzystorów w ich strukturach.

Układy sekwencyjne, których bazą są przerzutniki, działają nieco inaczej: przechowują dane pomiędzy kolejnymi cyklami zegara taktującego ich pracę. Z drugiej jednak strony, wiele zadań obliczeniowych można wykonać znacznie prościej (mniejszą liczbą tranzystorów), jeżeli rozłoży się je na poszczególne etapy i wykona je jeden po drugim.

Dzisiejsze systemy cyfrowe są połączeniem obu tych technologii. Bloki kombinacyjne przetwarzają możliwie dużą liczbę informacji, a synchroniczne przechowują je pomiędzy kolejnymi taktami zegara. To pewien kompromis. Dzisiejsze procesory czy mikrokontrolery pracują właśnie w ten sposób. Ale jest pewna grupa układów, które warto omówić oddzielnie.

Proste układy scalone

W sprzedaży są dostępne układy scalone, które zawierają w swojej strukturze kilka bramek logicznych. Po doprowadzeniu do nich odpowiedniego zasilania, będą realizowały swoje zadania - opis znajduje się w nocie katalogowej każdej z nich. Układy serii 7400 odpowiadają opisanemu wcześniej standardowi TTL. Z kolei, układy serii 4000 to układy zrealizowane w technologii CMOS.

Można je połączyć tak, aby realizowały dowolną funkcję. W ten sposób da się zbudować użyteczne urządzenia, na co dowodem są te kity:

Układy przetwarzające sygnały cyfrowe (DSP)

Jednak producenci dążą do zwiększenia udziału układów kombinacyjnych - na przykład, w algorytmach mnożenia liczb, zwłaszcza zespolonych. Te operacje są bezustannie wykonywane przez tzw. procesory sygnałowe, czyli układy scalone wyspecjalizowane w cyfrowym przetwarzaniu sygnałów. Realizują wiele zadań: od prostych, jak filtracja, do bardziej złożonych, na przykład rozpoznawanie mowy lub obrazów.

Każde z tych zadań wymaga wielokrotnego wykonania mnożenia. Dotychczasowe podejście, polegające na rozłożeniu każdej takiej operacji na kilka etapów, spowalniało cały proces. Dzisiejsi inżynierowie, przy wsparciu matematyków, próbują tak przekonstruować proces mnożenia dwóch liczb zespolonych, aby mógł on zostać wykonany możliwie szybko.

FPGA

Field-Programmable Gate Array - czyli bezpośrednio programowalna macierz bramek. Te układy zawierają w swojej strukturze sieć bramek i innych elementów logicznych, których strukturę można konfigurować poprzez programowanie. Docelowy układ połączeń zostaje zapisany w nieulotnej pamięci układu FPGA.

Zaletą tego typu układów, w porównaniu z tradycyjnymi mikrokontrolerami, jest znacznie większa liczba możliwości. W mikrokontrolerach każdy algorytm, na przykład dodawania czy sumowania, został opracowany i zaimplementowany przez producenta. Układy FPGA wykazują zdecydowanie większą elastyczność w tym zakresie, gdyż problem możemy rozwiązać według swojego upodobania.

Podsumowanie

Bramki logiczne, pomimo swojej prostoty, nadal stanowią fundament dzisiejszej elektroniki. Nie mógłby bez nich funkcjonować nawet najprostszy układ cyfrowy. Zostały na pewien czas zepchnięte na margines, lecz dzisiaj znów wracają do łask - inżynierowie widzą w nich nadzieję na dalsze przyspieszenie przetwarzania informacji.

Bramki realizują funkcje logiczne, których mamy kilka rodzajów. Każda z nich działa w inny sposób. Budowa bramek również może być różnoraka: od energooszczędnej technologii CMOS, przez prostą TTL po szybką ECL.